Квадратурный инкрементальный энкодер
 | Автор предупреждает! Статья не дописана! Данная статья не дописана и требует до- или, даже, переработки. Примеры и данные в этой статье могут быть не проверены, тесты не отлажены, а информация не действительна. Я постараюсь, чтобы таких статей было по-меньше, но пока они есть. Смотрите: NikiWiki:Отказ от ответственности |
Квадратурный инкрементальный энкодер - статья на русской WikiPedia устройство, позволяющее преобразовывать движение в импульсы. Существует множество разновидностей исполнения этих устройств. Но лично мне важен принцип их работы.
Содержание
Описание работы
Для простоты понимания рассмотрим измерительную линейку-энкодер (энкодер выполненный в виде датчика угла поворота вала подробно описан в предложенной выше статье с русской Wikipedia).
Обычно энкодер содержит два выходных сигнала. В зависимости от модификаций они могут быть TTL или CMOS уровней. Попавшая мне в руки линейка DC11 имеет питание 5 вольт и уровни сигнала 5 вольт.
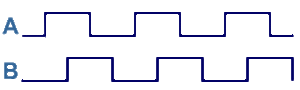
На картинке представлен график работы сигналов при равномерном движении датчика по линейке энкодера.
Легко видеть, что сигнал B отстает от сигнала А ровно на 1/2.
Таким образом мы можем получить 3 основных режима контроля движения при помощи энкодера (алгоритмов работы квадратурного декодера).
1х режим
В этом режиме контролируется лишь один сигнал - A. Но данный сигнал не дает нам понятия о том, в какую сторону движется датчик. Слева направо или наоборот. Для определения направления используется сигнал B. При этом, если посмотреть на график, то, если, предположить, что движение происходит слева направо, и мы фиксируем передний фронт сигнала A, то в этот момент сигнал B будет иметь противоположенное значение. Т.е. если А становится 1, и B в этот момент 0 - мы движемся справа налево. Обратное утверждение верно. Если сигнал А из 0 превратился в 1, а B при этом 1, то движение происходит слева направо.
Данный алгоритм вполне хорошо себя показывает, даже если датчик колеблется с очень небольшой амплитудой. В этом случае счетчик, ведущий подсчет смещения энкодера будет прирастать и убавляться на 1 при каждом колебании. Конечно, достаточном для срабатывания датчика.
Точность этого метода равна цене деления энкодера. Иными словами, если энкодер имеет 1000 меток на 1мм (точность 1мкм), то мы получим данные счетчика с точностью 1мкм.
Псевдокод функции, срабатывающей на прерывание счетчика будет выглядеть так:
A=B ? count-- : count++;
2x режим
Режим при котором контролируется как передний, так и задний фронт сигнала. В этом случае направление движения определяется тем же способом. С одним лишь исключением: алгоритмы определения направления "зеркальны" для переднего и заднего фронта сигнала A. Рассмотрев такой метод контроля энкодера мы можем прийти к выводу, что алгоритм из предыдущего раздела можно немного упростить и переписать иначе: если в момент перехода сигнала A в какое угодно состояние сигнал B противоположен - движение происходит вправо, а если совпадает, то влево (направления указаны согласно рисунка).
В этом случае точность контроля удваивается. Ибо на каждый физически возможный импульс датчика мы фиксируем и момент перехода датчика A из 1 в 0 и из 0 в 1. И, имея линейку с точностью 1мкм (1000 импульсов на 1мм) мы получим точность равную 2000 импульсов, т.е. 0.5мкм.
Как ни странно, но псевдокод функции, срабатывающей на прерывание счетчика будет выглядеть так же:
A=B ? count-- : count++;
4x режим
В этом режиме мы будем анализировать все 4 фронта (два фронта сигнала A и два фронта сигнала B). Легко видеть, что в этом случае точность измерений становится в 4 раза выше реальной точности линейки.
В этом режиме потребуется либо вызывать два разных прерывания, либо проверять условием какой из сигналов сработал. Поскольку логика определения направления для сигналов A и B прямо противоположена:
void intA() {
A==B ? count-- : count++;
}
void intB() {
A==B ? count++ : count--;
}
Или, при условии использования одного прерывания и одной функции (с точки зрения издержек на выполнение вызова функции это может быть значительно выгоднее, но требует дополнительно хранить предыдущее состояние сигналов):
void intAB() {
prevA==A ? calling=B | calling=A;
if (calling == A)
A==B ? count-- : count++;
else
A==B ? count++ : count--;
prevA=A;
}
Можно выдумать массу вариантов, при которых можно изрядно сэкономить алгоритм. Начиная от хранения переменной prevA (а это всего 1 бит) в регистре процессора (ведь контроль энкодера будет одним из основных заданий процессора). Контролировать обе переменные не требуется, ведь если не изменилась А, но мы попали в тело прерывания, которое срабатывает исключительно на сигналы A и B, то зачем проверять изменилась ли B? Энкодер нам предоставляет гарантию того, что одновременно 2 сигнала не сработают. Конечно, если мы не допустим того, чтобы скорость движения датчика, а, следовательно и частота следования импульсов была больше чем максимально допустимая скорость вызова и обработки прерывания.
Из этого мы можем вывести некоторую формулу f(s) описывающую необходимую частоту процессора при заданной максимальной скорости движения датчика энкодера.
f(s) = (1/Freq)*intTicks;
где:
- f - название функции, я так захотел;
- s - скорость движения датчика;
- Freq - частота процессора
- intTicks - издержки на полный цикл вызова и выполнения функции прерыавния включая все издержки на возможное переключение контекста и другие "процессорные" штучки.
Или. Иными словами. Если датчик движется со скоростью 1мм/сек (1000/2000/4000 контролируемых импульсов при трех возможных алгоритмах подсчета), то частота процессора должна быть не меньше чем количество подсчитываемых импульсов умноженное на суммарное время вызова прерывания в тактах.
Предположим, что функция intAB() требует от появления события до возврата из функции 28 тактов. Следовательно, для подсчета 1000 импульсов частота работы процессора должна быть не меньше чем 1000*28= 28000 (или 28кГц). Соответственно для режима 4x частота процессора должна быть в 4 раза выше т.е. 112кГц.
При этом и при такой постоянной скорости движения процессора больше у него ни на что времени хватать не будет. Но, поскольку пример не рассматривает ничего другого, то предположить каким должен быть запас производительности процессора невозможно. Однако, можно сделать вывод, что оптимизация числа тактов, необходимых для обработки прерывания должна быть выполнена на самом высоком уровне. Либо должны применяться аппаратные средства, например аппаратный таймер.
N (или R или Z) метки
В линейных энкодерах существует практика установки дополнительной шкалы (и соответствующего сигнала) аналогичного сигналу Z датчика угла поворота. Но в линейных энкодерах они устанавливаются не в единственном экземпляре, а повторяются с определенным интервалом. В случае, с попавшими мне в руки линейками DC11 - каждые 100мм. Причем первый находится в непосредственной близости от одного из краев линейки. Соответственно последний от края линейки может отстоять сколь угодно далеко.
Основная цель такого сигнала - контроль ошибок и установка линейки в нулевое состояние.
При этом используется 2 сигнала управления, кроме, собственно, таймера/прерывания для сигналов А и B. Один из этих сигналов "просит" контроллер линейки включить режим калибровки/сброса на "0" при первом поступившем сигнале N. А второй сигнал - от контроллера линеек к компьютеру, сообщающий о том, что сигнал был найден и в этот момент линейка счетчик линейки был сброшен. Прелесть этого алгоритма заключается в том, что немедленная остановка не требуется. Поскольку, даже, если датчик проехал дальше, то счетчик уже будет содержать расстояние от метки до текущей позиции. При такой точности позиционирования повторная калибровка не требуется. Контроллер уже точно знает где находится первая метка и с какой стороны она была найдена (левее текущей позиции или правее, т.е. счетчик положителен или отрицателен).
Второе применение меток - контроль ошибки. Если каждые 100мм расположена метка, то легко предположить, что расстояние между метками должно быть кратно числу подсчитываемых импульсов на этом расстоянии. В нашем случае это 1000 или 2000 или 4000 умноженные на 100. Т.е. 100 или 200 или 400 тысяч единиц от одной метки до другой. В случае, если встречена метка N, а число импульсов не кратно суммарной величине импульсов, должна выполниться процедура коррекции. Однако, коррекция должна производиться PID контроллером и контролирующим все передвижения устройством ибо если коррекция будет значительной и будет внесена автоматически, то управляющая программа может принять не верное решение в момент "перескока" значения счетчиков положения. Стоит также учитывать тот факт, что, в контексте станка с ЧПУ, управляющая программа и деталь, которая с ее помощью изготавливается, может находиться в пределах между двумя метками N и ни разу за все время работы программы не скорректироваться. Ввиду чего накопленная ошибка, связанная с возможными потерями импульсов может быть очень велика. В связи с вышеизложенным стоти предусмотреть в программе "отъезд" к точке расположения метки N каждые несколько циклов работы управляющей программы. В этом случае корреткировка будет вноситься постоянно и общая накопленная ошибка не будет слишком сильно влиять на точность изготовленной детали.
Размерность счетчиков
Для определения размерности переменной-счетчика энкодера нужно произвести не очень сложный расчет, а именно: для выбранного режима работы (1х, 2х или 4х) рассчитать число возможных значений счетчика. Например, для режима 4х и линейки длинной 670мм мы имеем:
4000*670=2680000
Подобное число может уместиться в слове из 22 бит. Иными словами, в одном 32х битном числе может быть расположен и счетчик положения и значение ошибки и направление и значения сигналов А и Б в момент времени считывания. Предположим, что ошибка не превышает 1% (а иначе, зачем нам линейки?), тогда размерность ошибки будет 2^15.